Chapter 9 - Consistency and Consensus

Consistency Guarantees

• Eventual Consistency - Means the system will eventually catch up after a unspecified amount of time. It’s a weak form of consistency.
• There exists stronger consistency models, which come there own potential cons such as performance and availability. Though they are easier to use correctly.

Linearizability

• Main idea behind linearizability i.e. the system appears as if there is only one copy of the data and all operations on it are atomic. Even though in reality there are multiple replicas, the application doesn’t need to worry about them.

• Linearizability is a recency guarantee, meaning once a write is successful, all subsequent reads will return the most recent write.

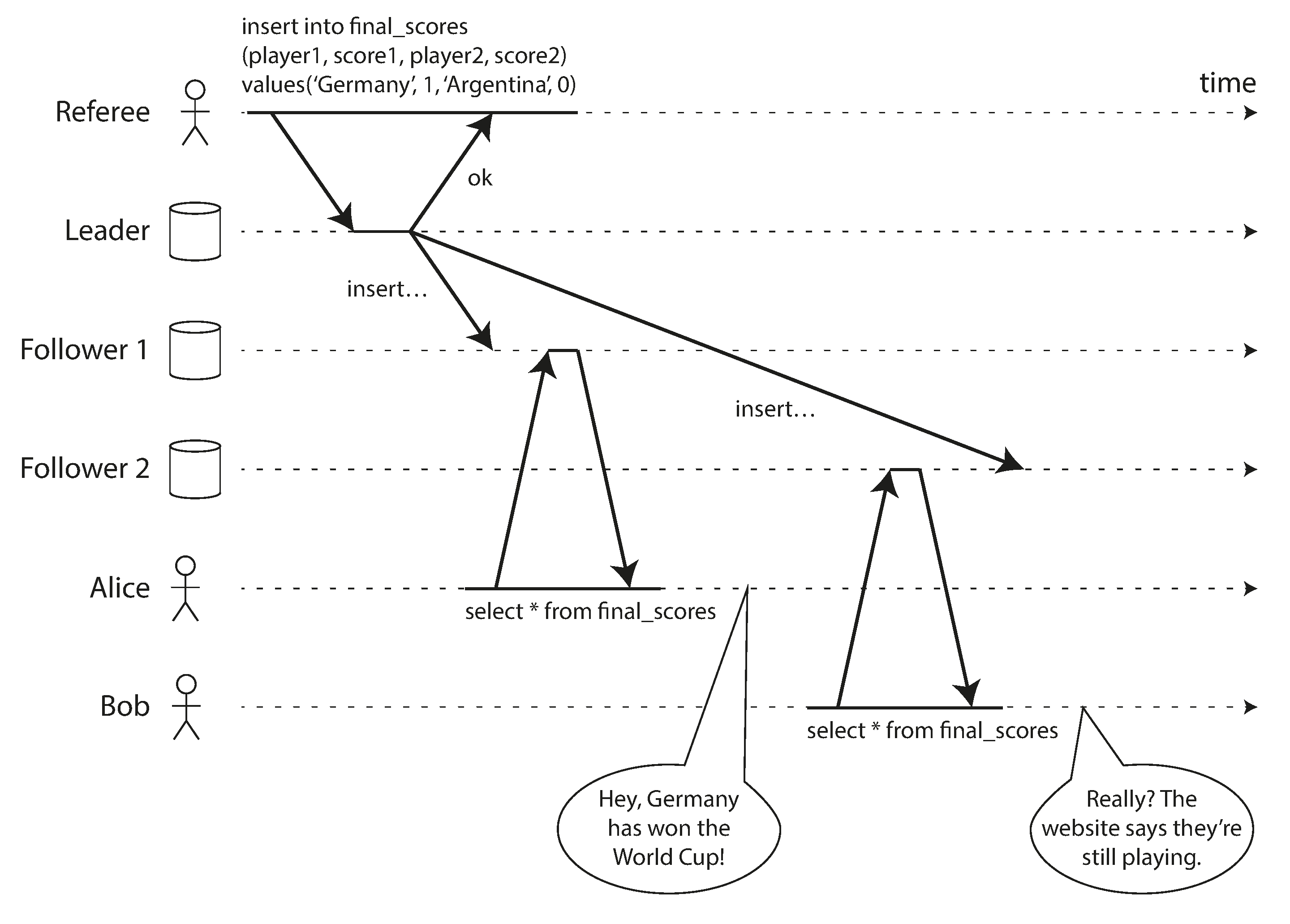
• What Makes a System Linearizable - On the surface it seems the idea behind linearizability is simple, but as it’s said “devil lies in the details”.

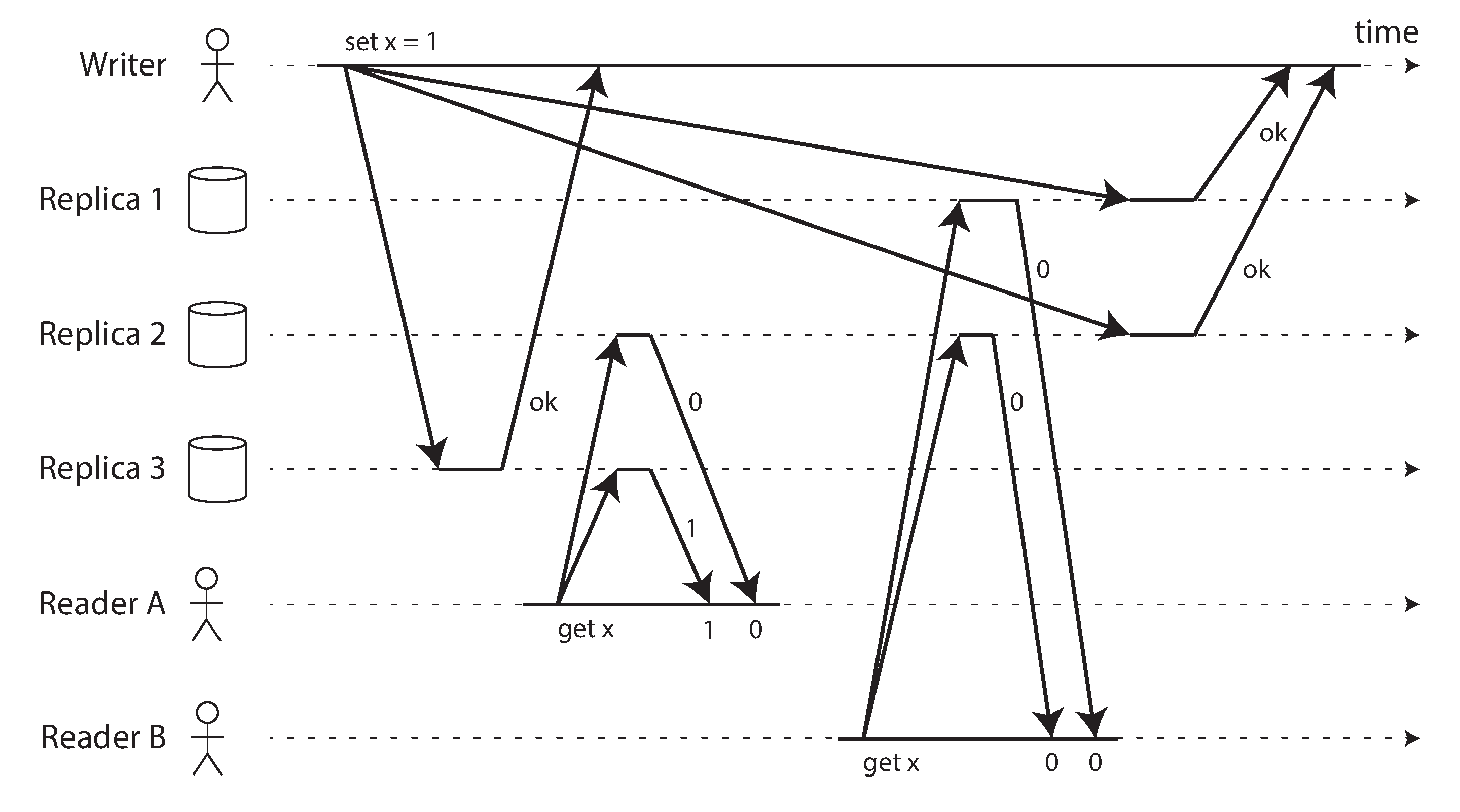
  • If a read request is concurrent with a write request, it may return either the old or the new value. Readers could be flipping between the old and new values which is not linearizable. We need to add another constraint to make it linearizable.
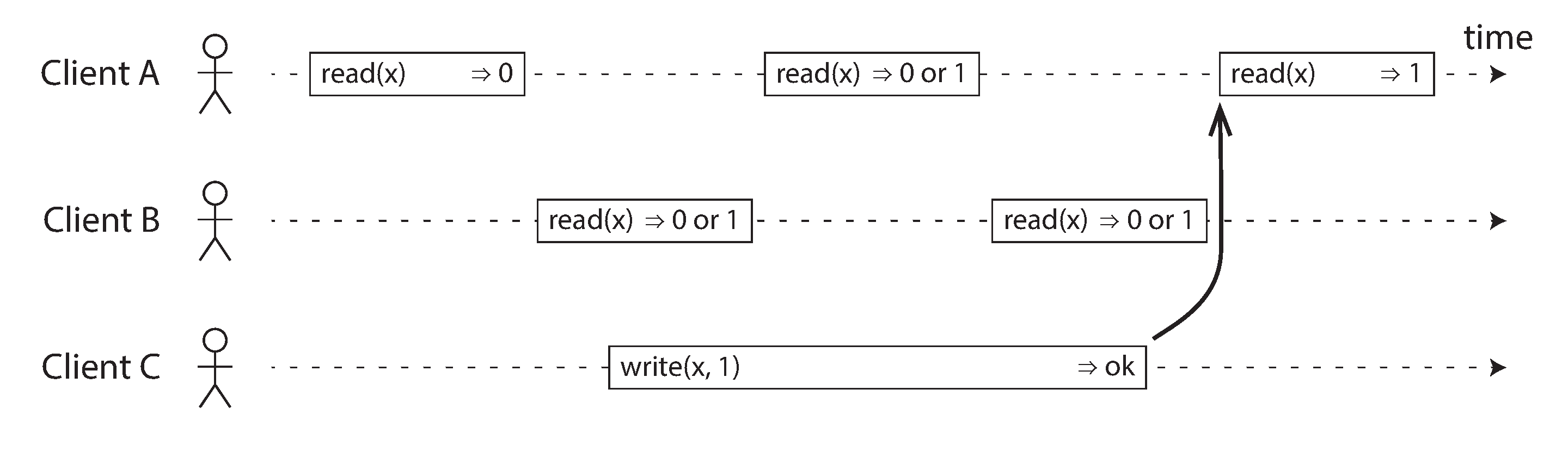
  • After any one read has returned the new value, all following reads must also return the new value
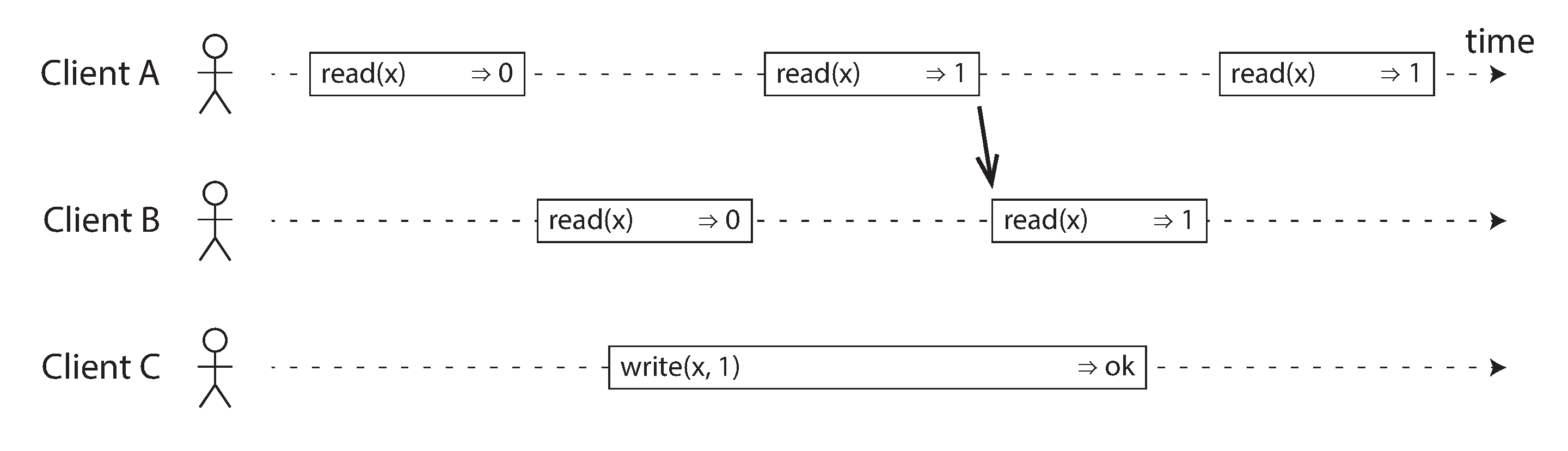
  • Visualising the points in time at which the reads and writes appear to have taken effect. The final read by B is not linearizable.
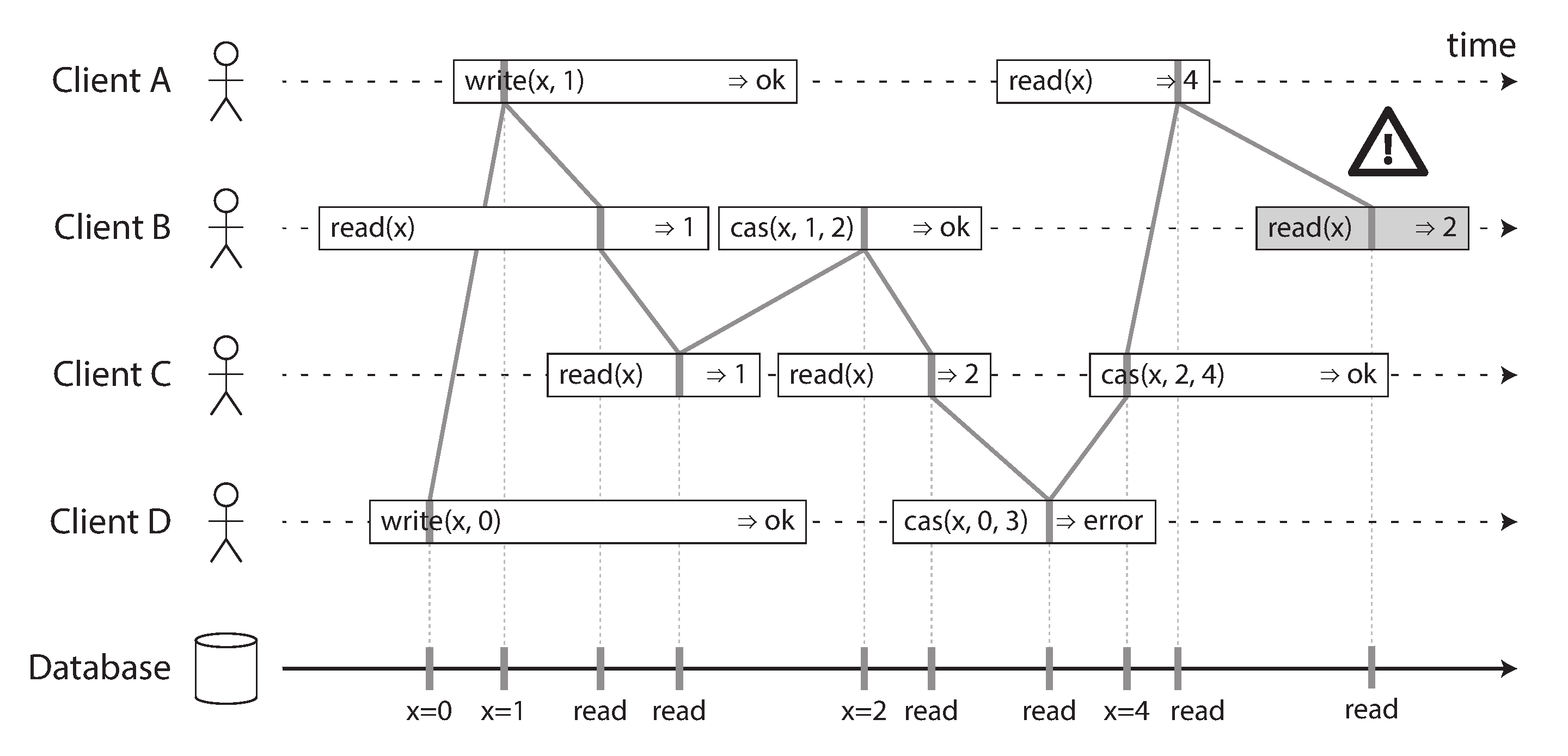
  • It is possible (though computationally expensive) to test whether a system’s behaviour is linearizable by recording the timings of all requests and responses, and checking whether they can be arranged into a valid sequential order.link

• Linearizability vs Serializability

  • Serializability - Isolation property of transactions. It guarantees that transactions behave the same as if they had executed in some serial order (each transaction running to completion before the next transaction starts).
  • Linearizability - It is a recency guarantee on reads and writes of a register(an individual object).
  • A database with both serializability and linearizability is said to be strict serializability or strong one-copy serializability.

• Cross-channel timing dependencies

  • The web server and image resizer communicate both through file storage and a message queue, opening the potential for race conditions.
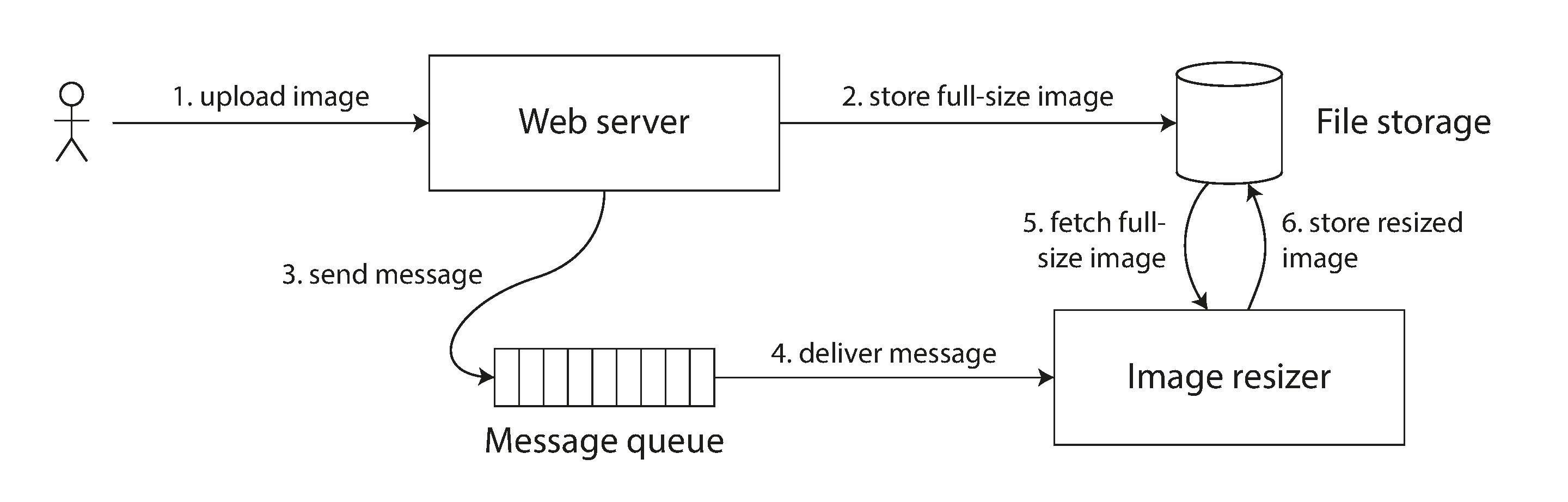
  • If the file storage service is linearizable, then this system should work fine. If it is not linearizable. there is the risk of a race condition: the message queue might be faster than the internal replication inside the storage service. In this case, when the resizer fetches the image, it might see an old version or nothing at all. If it processes and old version of the image, the full-size and resized images in the file storage become permanently inconsistent.

• Implementing Linearizable Systems

  We want system to be fault-tolerant too, let’s see the various replication methods to see if they can be linearizable.

  • Single-leader replication(potentially linearizable) - Making reads from the leader, or from synchronously updated followers, they have the potential to be linearizable.
  • Consensus algorithms(linearizable) - Prevent split brains and stale replicas. This is how ZooKeeper and etcd work.
  • Multi-leader replication(not linearizable) - Concurrently process writes on multiple nodes and asynchronously replicate them to other nodes. Hence, they can produce conflicting writes that require resolution.
  • Leaderless replication(probably not linearizable) - You can potentially obtain “strong consistency” by requiring quorum reads and writes(w + r > n). “Last write wins” conflict resolution methods based on time-of-day clocks are almost certainly non-linearizable, because clock timestamps cannot be guaranteed to be consistent with actual event ordering due to clock skew.

• Linearizability and quorums

  • It is possible to make Dynamo-style quorums linearizable at the cost of reduced performance: a reader must perform read repair synchronously, before returning results to the application and a writer must read the latest state of a quorum of nodes before sending its writes.
  • Raik doesn’t but Cassandra does use it. Though Cassandra uses a “last write wins” conflict resolution strategy, which is not linearizable.
  • Only linearizable read and write operations can be implemented in this way; a linearizable compare-and-set operation cannot, because it requires a consensus algorithm.

• The Cost of Linearizability

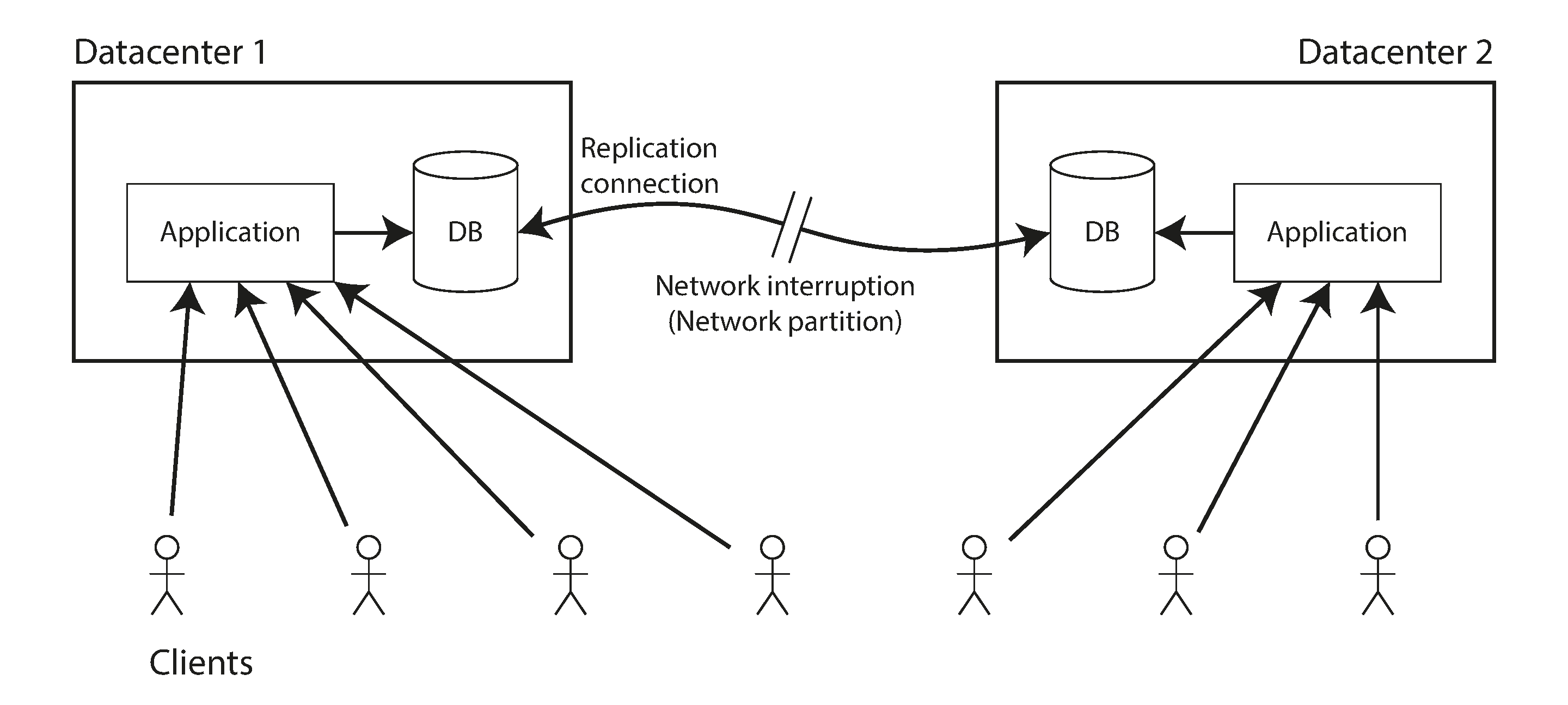
  A network interruption forcing a choice between linearizability and availability.

  • CAP theorem
    • If your application requires linearizability, you must accept that it will become unavailable in the event of a network partition. Either you can return an error or wait for the network to heal.
    • If your application does not require linearizability, you can choose to continue operating during a network partition, but you must accept that your system would be not linearizable but available.
    • It is sometimes presented as Consistency, Availability, Partition tolerance, pick two. Seems misleading since network partition is a fault not something you can choose to have or not have.
    • When network is working correctly, a system can provide both consistency(linearizability) and availability. When network fault occurs, you have to choose between either linearizability or total availability.
  • Linearizability and network delays
    • Although linearizability is a useful guarantee, surprisingly few systems are actually linearizable in practice. For example, even RAM on a modern multi-core CPU is not linearizable, since every CPU core has its own cache and store buffer.
    • Many distributed databases that choose not to provide linearizable guarantees: they do so primarily to increase performance, not so much for fault tolerance.link
    • Linearizability is slow-and this is true all the time, not only during a network fault.

Ordering Guarantees

• Ordering is something we have run into before throughout this book -

  • Replication log - order of writes. In case of no single leader, conflicts can occur due to concurrent writes (ways to handle them: mentioned in “Handling Write Conflicts” section).
  • Serializability - ensure that transactions behave as if they were executed in some sequential order. One way to achieve this is by literally executing transactions in a serial order. Other way is to allow concurent execution while preventing serialization conflicts by using locks (2 phase locking) or aborting (if needed like in Serializable Snapshot Isolation).
  • Use of timestamps and clocks which was covered in chapter 8 to order events.

• Ordering and Causality

  • Ordering helps preserve causality. Few examples we have seen where causality has been important:
    • “Consistent Prefix Reads” - The observer saw first the answer to a question, and then the question being answered.
    • Replication between leaders and noticed that some writes could “overtake” others due to network delays. Leading to one of the replicas seeing a row getting updated which doesn’t exist yet.
    • In the context of “Snapshot Isolation and Repeatable Read”, a transaction reads from a consistent snapshot. “Consistent” here means consistent with causality: if snapshot contains an answer, it must also contain the question. Read skew(non-repeatable reads) means reading data in a state that violates causality.
    • Serializable Snapshot Isolation detects write skew by tracking the causal dependencies between transactions.
  • If a system obeys the ordering imposed by causality, it is said to be causally consistent.
  • Total Order - Allows any two elements to be compared, so if you have a set have two elements, you can always say which one is greater and which one is smaller. For example - natural numbers.
  • Partial Order - Two events are ordered if they are causally related (one happened before the other), but they are incomparable if they are concurrent.
  • Linearizability is a total order, but causality is a partial order.
  • There no concurrent operations in a linearizable datastore: there must be a single timeline along which all operations are totally ordered.
  • Distributed version control systems such as Git, their version histories are very much like the graph of causal dependencies. Often one commit happens after another, in a straight line, but sometimes you get branches and merges are created when those concurrently created commits are combined.
  • Any system that is linearizable will preserve causality.
  • Making a system linearizable can harm its performance and availability as we have seen in the previous section.
  • Causal consistency doesn’t need to be linearizable, plus it does not slow down due to network delays and remains available during network partitions.
  • Causal consistency needs to track causal dependencies across the entire database, not just for a single key. Version vectors can be generalized to do this.

• Sequence Number Ordering

  • We can use sequence numbers or timestamps to order events. Here timestamps are from logical clocks and not time-of-day clock which are unreliable(covered in chapter 8).
  • These provide a total order and are compact(only a few bytes in size).
  • With single-leader replication, the leader can simply increment a counter for each operation and thus assign a monotonically increasing sequence number to each operation in the replication log.
  • Noncausal sequence numbers - With non-single leader system like multi-leader, leaderless or database is partitioned how to generate sequence numbers for operations. Few methods -
    • Each node can generate its own sequence numbers independently, like odd and even generators are separate.
    • Attach timestamp from physical clock to each operation, if they are high resolution could provide total order.
    • Preallocate a range of sequence numbers to each node.
    • These methods perform better and are more scalable than pushing all operations through a single leader that increments a counter. But the sequence numbers they generate might not be consistent with causality.
    • Each node process operations at different speed, leading to odd/even generators falling behind.
    • Timestamps from physical clocks can be inconsistent due to clock skew.
    • Preallocated range of sequence numbers, one operation may be given a sequence number in higher range vs another operation which actually happened later but got a lower sequence number.
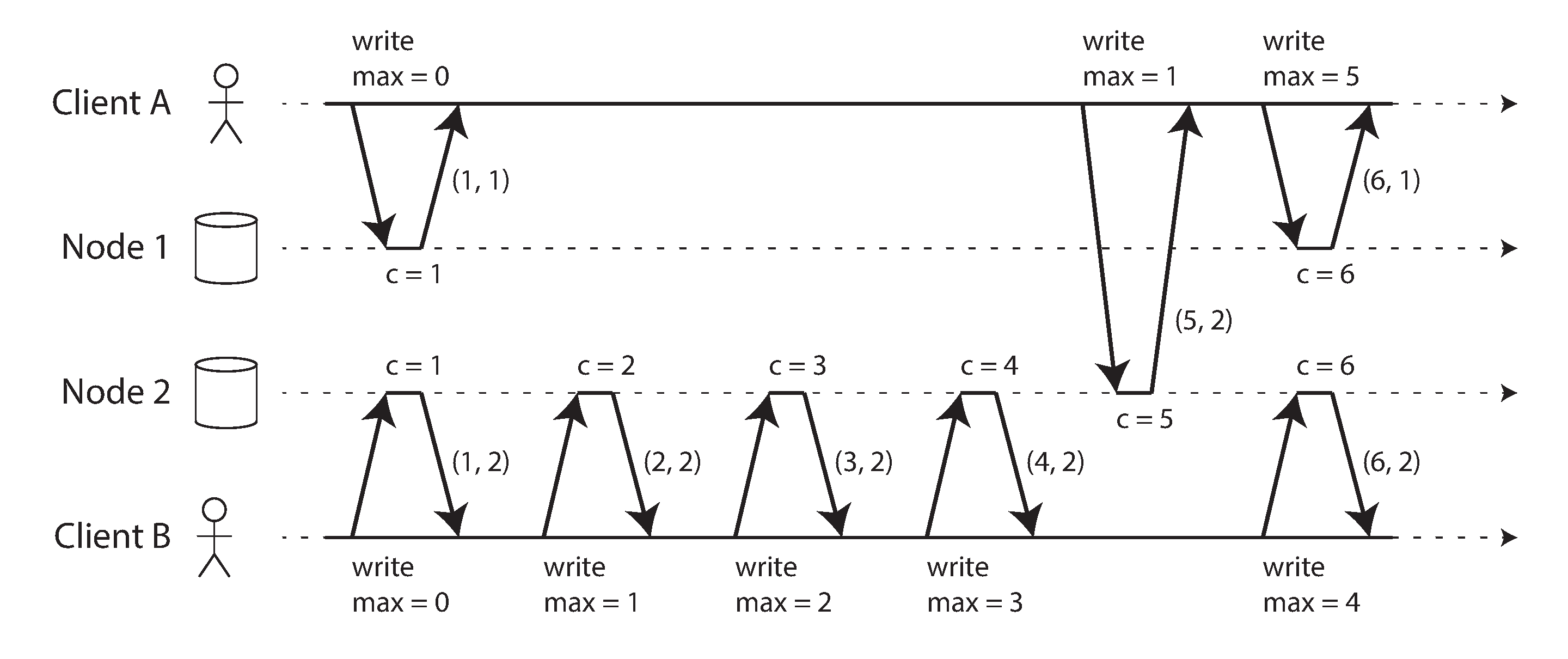
  • Lamport Timestamps
    • Each node has a unique identifier and each node keeps a counter of the number of operations it has processed.
    • Every node and every client keeps track of the maximum counter value it has seen so far, and includes that maximum on every request. When a node receives a request or response with a maximum counter value greater than its own counter value, it immediately increases its own counter to that maximum.
    • This lecture really helped me understand it more clearly.
    

• Total Order Broadcast

  • A protocol for exchanging messages between nodes. It requires two safetly properties always be satisfied:
    • Reliable delivery - No messages are lost: if a message is delivered to one node, it is delivered to all nodes. Even though delayed at times due to network interruptions.
    • Totally ordered delivery - Messages are delivered to every node in the same order.
  • The order is fixed at the time the messages are delivered: a node is not allowed to retroactively insert a message into an earlier position in the order if subsequent messages have already been delivered. This fact makes total order broadcast stronger than timestamp ordering.
  • Implementing linearizable storage using total order broadcast
    • Total order broadcast is asynchronous: messages are guaranteed to be deivered reliably in a fixed order, but there is no guarantee about when a message will be delivered. By contrast, linearizability is a recency guarantee: a read is guaranteed to see the latest write.
    • If multiple users try to concurrently grab the same username, only one of the compare-and-set operations will succeed, because the others will see a value other than null(due to linearizability). Such a linearizable compare-and-set operation can be implemented using total order broadcast as an append-only log.
    • Reads are not necessarily linearizable since the the replicas are updated asynchronously. Few ways to make reads linearizable -
      • Sequence reads through the log by appending a message, reading the log, and performing the actual read when the message is delivered back to you. Quorum reads inh etcd work somewhat like this.
      • Read from a replica that is synchronously updated on writes and is thus sure to up to date.
  • Implementing total order broadcast using linearizable storage
    • For every message you want to send through total order broadcast, you increment-and-get the linearizable integer, and then attach the value you got from the register as a sequence number to the message. You can then send the message to all nodes(resending any lost messages), and the recipients will deliver the messages consecutively by sequence number.
    • Unlike Lamport timestamps, the numbers you get from incrementing the linearizable register form a sequence with no gaps. Thus, if a node delivered message 4 and receives an incoming message with sequence number of 6, it knows that it must wait for message 5 before it can deliver message 6.